Números Triangulares

Olá Olá, senhores.

Hoje eu venho falar sobre uma das atividades que mais me deram certo, que foi a dos números triangulares e Quadrados. É uma das atividades mais simples e intuitivas, entretanto que melhor motiva os alunos pelo apelo geométrico simples.

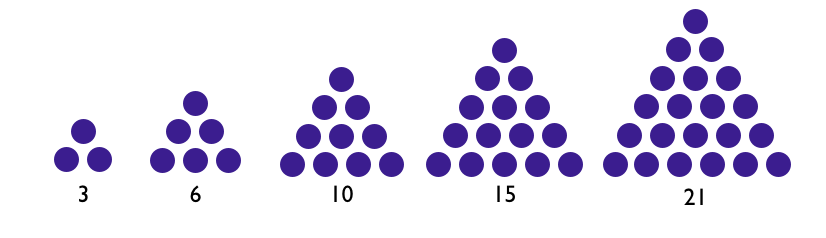
Eu gosto de iniciar essa aula com um ar de mistério, do tipo "Crianças, vocês sabiam que existem alguns números especiais, que tem formas geométricas??". Em geral, o primeiro instinto deles é pensar no algarismo ao invés do número, e esse é um bom ponto para uma discussão inicial, qual a diferença entre o número nove e o algarismo '9'. Passada essa fase inicial de discussão sobre a natureza dos números, eu começo mostrando pra eles que o 3 é um número com o seu desenho. Segue uma discussão sobre a existência de outros números triangulares, e após algumas propostas, eventualmente essa sequencia aparece no quadro:

Uma boa primeira observação que é importante que eles notem é o tamanho da base. Eu gosto de chamar atenção para essa questão perguntando se existe algum número triangular faltando nessa sequencia, por exemplo entre o 3 e o 6, ou entre o 6 e o 10. Para que eles compreendam o padrão, usualmente eu chamo atenção para o comprimento da base, que segue a ordem 2, 3, 4, 5, ... Nesse ponto, talvez alguém proponha, ou talvez não, mas é bom possuir o número triangular 1, representado por apenas uma bolinha e cuja base tem comprimento 1. Uma vez que eles vejam que não pode haver "meias bolinhas" na base, eles vão ver que, de fato, não há nenhum número triangular entre estes apresentados. Então a questão se volta para como encontrar os próximos números triangulares.

Enquanto se buscam números triangulares cada vez maiores, é importante administrar a competição e não deixar que poucas pessoas dominem a conversa enquanto outros se sintam perdidos. É possível conseguir que a turma inteira fique interessada querendo adivinhar qual é o próximo número triangular, e só isso já é o bastante para conduzir uma aula inteira. Chame sempre atenção para o padrão, e várias propostas interessantes vão surgir.

"Será que são os múltiplos de 3?"
"Segue 10, 15... será que o próximo é 20, já que é +5?"
" Todos são ímpares, né, tio?"

Conduza essas abordagens e veja onde elas falham, onde dão certo e siga conduzindo a discussão, deixando que eles mesmos verifiquem se estão certos. Pedir para que eles desenhem numeros triangulares cada vez maiores no quadro também faz a aula ficar mais interativa e divertida.

Eventualmente eles vão querer arrancar de você qual é o padrão. Então, quando a turma chegar nesse ponto de buscar um padrão, procure faze-los conectar um número triangular ao anterior. Em geral eles costumam encontrar o desenho anterior no topo do seguinte, conforme o desenho:

O interessante é que eles descubram que para pegar o quarto número triangular e construir o quinto, basta pegar o 10 (quarto número triangular) e somar mais 5 (pois estamos construindo o quinto). Depois de brincar com esse padrão um pouco, eles serão capazes de construir números triangulares cada vez maiores.

Essa classe possui duas continuações naturais possíveis:

A primeira seria explorar outras formas de números, como os números quadrados e pentagonais e hexagonais, e brincar com as relações entre eles.

A outra seria procurar números triangulares grandes, sem precisar construir os anteriores. Essa conduziria naturalmente a pergunta 1 + 2 + 3 + 4 + ... + N, que já é outra aula do círculo. Um bom exemplo seria iniciar uma classe seguinte com

"Turma, voces lembram dos números triangulares? Então, eu gostaria de saber qual é o vigésimo número triangular."

Ao observar a forma como eles são construidos, a questão do 1+2+...+N aparecerá naturalmente, e é possível seguir pra essa classe.

Abraços e até mais, senhores

\o